ArtWare – Re-Enactment kybernetischer Kunst (2/2)

Fortsetzung von Teil 1.

1. Methodologie des Re-Enactments

Der zweite Teil des Kurses verfolgte das Ziel auf Basis der zuvor erarbeiteten Theorien – sowohl der Informationsästhetik als auch der Medienarchäologie – eine Re-Implementierung historischer Computergrafiken als Methode analytischer Mediengeschichtsschreibung anzuwenden. Zur Legitimation des Vorgehens wurde das Konzept des Re-Enanctments dazu zunächst aus drei Quellen hergeleitet: Robert Collingwoods (1947) Theorie “History as Re-Enactment”, Ian Bogosts (2012:85-112) “Carpentry” sowie Andreas Fickers (2015) “Hands-on! Plädoyer für eine experimentelle Medienarchäologie”. Kurz zusammengefasst ergaben sich aus der Diskussion dieser Konzepte folgende Überlegungen:

1. Nach Collingwood, entziehen sich historische Prozesse dem Historiker dadurch, dass er sie im Denken stets “vergegenwärtigt”. Seine Neu-Denken des historischen Prozesses nimmt nicht nur eine Bewertung, sondern auch eine Aktualisierung des Historems vor. Dieses ahistorische Moment findet sich auch in operativen Medien, die im Medienzustand radikal gegenwärtig sind (Ernst 2012:113) – selbst wenn sie historische Technologien sind oder vergangene Inhalte darbieten.
2. Theorie gewinnt durch “Carpentry” ein neues non-diskursives Aufschreibesystem und umgeht damit die problematischen Momente des Diskursiven (Verhandelbarkeit, Subjektivität, …) Das Experiment und die Demonstration stellen eigene Formen der non-diskursiven Theoriebildung dar und performieren technische Zeitlichkeiten und Strukturen, die nicht nur etwas über den Inhalt des Experiments, sondern auch über die Versuchsanordnung und die eingesetzten Medien aussagen.
3. In Abgrenzung zu Fickers lässt eine experimentelle Medienarchäologie (als Re-Enactment) keinerlei Aussagen über vergangene Nutzungsweisen und soziale Bedeutungen von Medientechnologien und -inhalten zu, weil sie (siehe Punkt 1) stets in der Gegenwart des Experimentierens stattfindet. Allerdings ermöglicht eine solche Medienarchäologie Reflexionen über die so produzierten Anachronismen (wenn historischen Medienprozesse in der Gegenwart nachvollzogen werden).

Vor dem Hintergrund dieser Erkenntnisse wird das Werkzeug, das für das Re-Enactment genutzt werden soll, zu einem “epistemischen Ding” (Rheinberger 2001:18-34): Es muss im Prozess des Experimentes stets als konstitutives Element mitgedacht werden und seine Rolle muss dabei zugleich die eines “Werkzeugs” wie eines “Zeugs” (Heidegger 1967:68-83) sein, das beim Nutzer in seiner (Be)Nutzung ein Wissen über sich selbst erzeugt.

2. BBC BASIC

Für die Implementierung der Grafiken wird eine ebenfalls “historische” Programmiersprache genutzt: BBC BASIC, das 1981 von der Firma Acorn für den Britischen Schulcomputer BBC Micro entwickelt wurde. BBC BASIC ist eine der unzähligen Dialekte der Programmiersprache BASIC, die bereits 1964 am Dartmouth-College für Studenten der Kunst- und Geisteswissenschaften entwickelt wurde und weitgehend von informatischen und mathematischen Konzepten abstrahiert. Die dem Assembler sehr nahestehende imperative Programmierung von BASIC, zumal mittels eines Interpreters, erleichtert das Erlernen von Programmiersprachen (etwa mittels trial&error-Verfahren) insbesondere für Autodidaktiker. BBC BASIC wird für unterschiedliche Plattformen bis heute weiterentwickelt und ermöglicht die Programmierung sowohl historischer Programmierparadigmen (imperativ, unstrukturiert) als auch den Einsatz moderner Konzepte (strukturiert, prozedural, objektorientiert). Darüber hinaus verfügt es über mächtige Grafik-Befehle, die die Implementierung der historischen kybernetischen Kunstwerke erleichtern können.

Der erste Programmierblock beinhaltete die Erarbeitung des BASIC-Befehlsvorrates, der grundsätzlichen Struktur von BASIC-Programmen sowie jener Elemente, die für die Programmierung von Grafik-Algorithmen zentral sind: Schleifen, bedingte Verzweigungen sowie mathematische Funktionen (insbesondere Pseudo-Zufallszahlen, Trigonometrie- und Iterationsfunktionen). Der zweite Programmierblock stellte dann die Grafikfunktionen von BBC BASIC vor: zunächst die Pseudografik-Programmierung (mittels Zeichensatzelemente und deren Positionierung auf dem Bildschirm), dann die Pixelgrafik (Punkte, Linien, geometrische Objekte sowie absolute und relative Positionierung). Die damit zusammenhängenden mathematischen Episteme (der Monitor als cartesisches Koordinatensystem oder als Gauß’scher Vektorraum, die Un/Möglichkeit der Zufallszahlengenerierung in deterministischen Maschinen) wurden dabei experimentell erprobt.

3. Heuristische Re-Enactments

Wie aber lassen sich kybernetische Kunstwerke in BBC BASIC nachprogrammieren, wenn deren algorithmische Grundlagen unbekannt sind? Selbst die Grundkenntnis einer Programmiersprache lässt heuristische Zugänge zu einer Lösung zu. Durch das bloße Betrachten der Grafiken, das Abmessen, Zählen und Nachverfolgen von dargestellten Objekten (den “einfachen Zeichen” [vgl. Nake 1974:59], wie sie in der Informationsästhetik genannt werden) lassen sich Algorithmen auf experimentellem Wege entwickeln, die ein Re-enactment möglich machen.

3.1 A first step

Abb. 1: A. Michael Noll “Vertical-Horizontal Number Three” (1965)

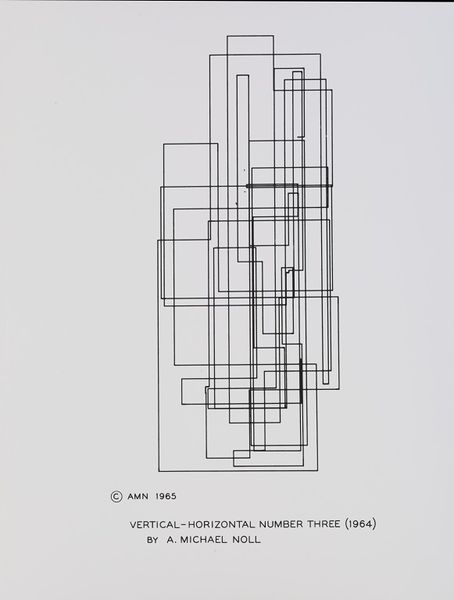
Für das erste Experimente wurde ein von verschiedenen Künstlern implementiertes Kunstwerk genutzt, das zufällig positionierte horizontale und vertikale Linien miteinander verbindet. A. Michael Nolls “Vertical-Horizontal Number Three” diente hierbei als Ausgangsobjekt:

1. Zunächst wurde geschätzt, aus wie vielen Linien die Grafik besteht.
2. Die Frage, ob der Linienzug einen Anfang und ein Ende besitzt, wurde beantwortet.
3. Es wurde überlegt, wie die Linien zueinander in Verbindung stehen.
4. Die Anzahl der Zeichendurchläufe wurde geschätzt.
5. Die Seitenverhältnisse des Bildes wurden gemessen.

Nachdem das Konstruktionsprinzip (Punkt 3) entdeckt war (Zeichen von Koordinate [x0/y0] zu [x1/y0] zu [x1/y1] zu [x2/y1] usw.) wurde ein erstes Programm geschrieben. Die Ausgabe zeigte, das zu viele Durchläufe angenommen wurden und dass das Bild zu nah am Rand gezeichnet wurde. Also wurde im nächsten Schritt die Anzahl der Iterationen reduziert und die Ausgabe mittels origin-Befehl umpositioniert. Nachdem das Ergebnis zufrieden stellte, wurde das Programm noch einmal modifiziert:

1. Es wurde eine tastaturgesteuerte Endlosschleife implementiert, um beliebig viele Varianten des Bildes zu zeichen.
2. Das Zeichnen der einzelnen Linien wurde mittels WAIT-Befehl verlangsamt, um den automatischen Konstruktionsprozess (und damit gegebenenfalls die Zufallszahlen-Verteilung) besser beurteilen zu können.

Im Ergebnis entstand folgender Code:

origin 100,100
x1=rnd(300)
y1=rnd(800)
move x1,y1
for i=1 to 50
   x2=rnd(300)
   y2=rnd(800)
   draw x1,y2
   wait 1
   draw x2,y2
   wait 1
   x1=x2:y1=y2
next i

Dieser Produzierte in einem Durchlauf die Grafik in Abb. 2.

Abb. 2: Eine Ausgabe des Re-Enactments von “Vertical-Horizontal Number Three”

3.2 Die Grenzen kybernetischen Re-Enactments

Das zweite Re-Enactment wurde von Georg Nees’ Bild “Locken” vorgenommen. Abermals wurde der Algorithmus mittels heuristischer Verfahren erstellt: Die Frage, welche “einfachen Zeichen” die Grundlage der Grafik bilden (Kreise) wurde beantwortet, die Anzahl und Größe der Kreise ermittelt und mit Hilfe des circle-Befehls ein einfaches Programm geschrieben.

Abb. 3: Georg Nees: “Locken” (1971)

Hierbei offenbarte sich die erste Hürde eines rein digitalen Re-Enactments. Konnte Nolls Grafik noch problemlos auf dem Bildschirm nachgezeichnet werden, so zeigte sich bei Nees’ Bild ein Effekt, der so nur durch die “hard copy” eines Plotters erreicht werden kann: Die dunklen Ränder des Bildes stammen offenbar von der Kollision des Zeichenstiftes mit dem Rand/Rahmen der Zeichenfläche. Dieser Effekt lässt sich bestenfalls, dann aber nur mit großem Aufwand, nachahmen. Im Kurs wurde vorgeschlagen das Ausgabefenster am Ende des Programmdurchlaufs so weit zu verkleinern, dass die Kreise am oberen und rechten Rand abgeschnitten werden.

Bei der Betrachtung von “Locken” kam zudem die Frage auf, ob das Bild möglicherweise in mehreren Durchgängen generiert worden ist. Auf Basis der Programmierkenntnisse entwickelte sich schnell die Überlegung, dass Nees die vier unterschiedlich großen Kreise wahrscheinlich in vier Durchläufen nacheinander aufs Papier hat zeichnen lassen. Also wurde das BBC-BASIC-Programm so entworfen, dass es vier Iterationen (je eine für eine Kreisgröße) nacheinander ausführt.

Die erste Implementierung zeigte, dass die Anzahl der Kreise unterschätzt wurde. Zudem erwies sich der repetitive Programmierstil, der vier sehr ähnliche Algorithmen nacheinander schaltete, als sehr zeitaufwändig. Also wurden mehrfach genutzte Elemente in Subroutinen ausgelagert (etwa die Zufallszahlengenerierung für die Kreismittelpunkte). Das Programm konnte so “verschlankt” werden und an die von Nees bevorzugte prozedurale Programmierung (in ALGOL) angenähert werden:

clg
for i=1 to 100
   gosub xy
   circle x,y,50
next i
for i=1 to 100
   gosub xy
   circle x,y,75
next i
for i=1 to 100
   gosub xy
   circle x,y,100
next i
for i=1 to 100
   gosub xy
   circle x,y,150
next i
end
(xy)
   x=rnd(350)
   y=rnd(850)
return

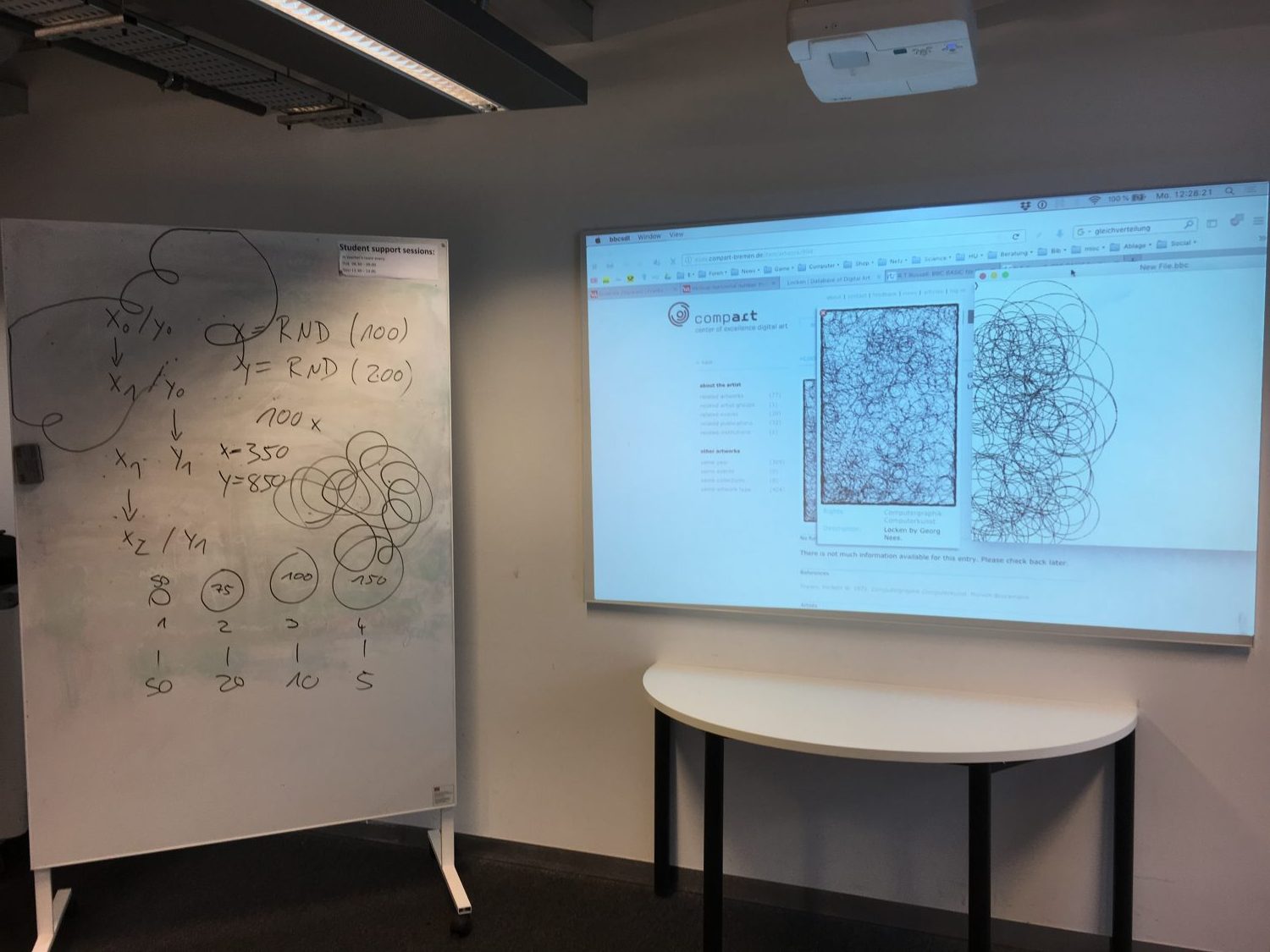
Abb. 4: Eine Ausgabe des Re-Enanctments von “Locken” und Tafelentwurf

3.3 Digital Tools

Für das dritte Re-Enactment wurde von Schwarzweiß- auf Farbgrafik gewechselt. Herbert W. Frankes Bild “Quadrate” wurde hierfür ausgewählt. Aufgrund der Erkenntnisse aus dem “Locken”-Re-Enactment wurde bereits bei der heuristischen Annäherung an das Original ein dreistufiger Entstehungsprozess angenommen: Die unterschiedlich großen und verschieden gefärbten Quadrate wurden wahrscheinlich in drei aufeinander folgenden Programmteilen gezeichnet.

Abb. 5: Herbert W. Franke “Quadrate” (1970)

Zur Ermittlung der Farben wurde ein digitaler Farbsensor auf die Bildschirmausgabe von “Quadrate” (Abb. 5) gelegt. Die so ermittelten RGB-Farbwerte wurden auf unterschiedliche colour-Stifte definiert. Zudem wurde die Größe der Quadrate in proportionaler Abhängigkeit zueinander (1:2:4) gemessen. Schließlich wurde geschätzt, wie viele der einzelnen Quadrate sich auf der gesamten Bildfläche befinden und welche Maße diese Fläche besitzt.

Auch hier erbrachte der ersten Programmdurchlauf, dass die Anzahl unterschätzt worden war. Überdies wurden die vier großen (schwarzen) Quadrate häufig so gezeichnet, dass sie über die Ränder der angenommenen Bildgröße hinaus ragten. Um diesen Umstand nicht algorithmisch korrigieren zu müssen, wurden das Programm mehrfach durchlaufen, bis alle vier großen Quadrate zufällig innerhalb des gedachten Rahmens platziert wurden. (Vgl. Abb. 6; dieses Verfahren wich sicherlich von dem Frankes ab, da seine Zeichnung einerseits auf Papier erstellt wurde und damit zu zeit- und materialaufwändig für solche Versuche war, und es andererseits die Papiergröße gar nicht zugelassen hatte, dass die großen Quadrate über den Rahmen hinaus gezeichnet werden.)

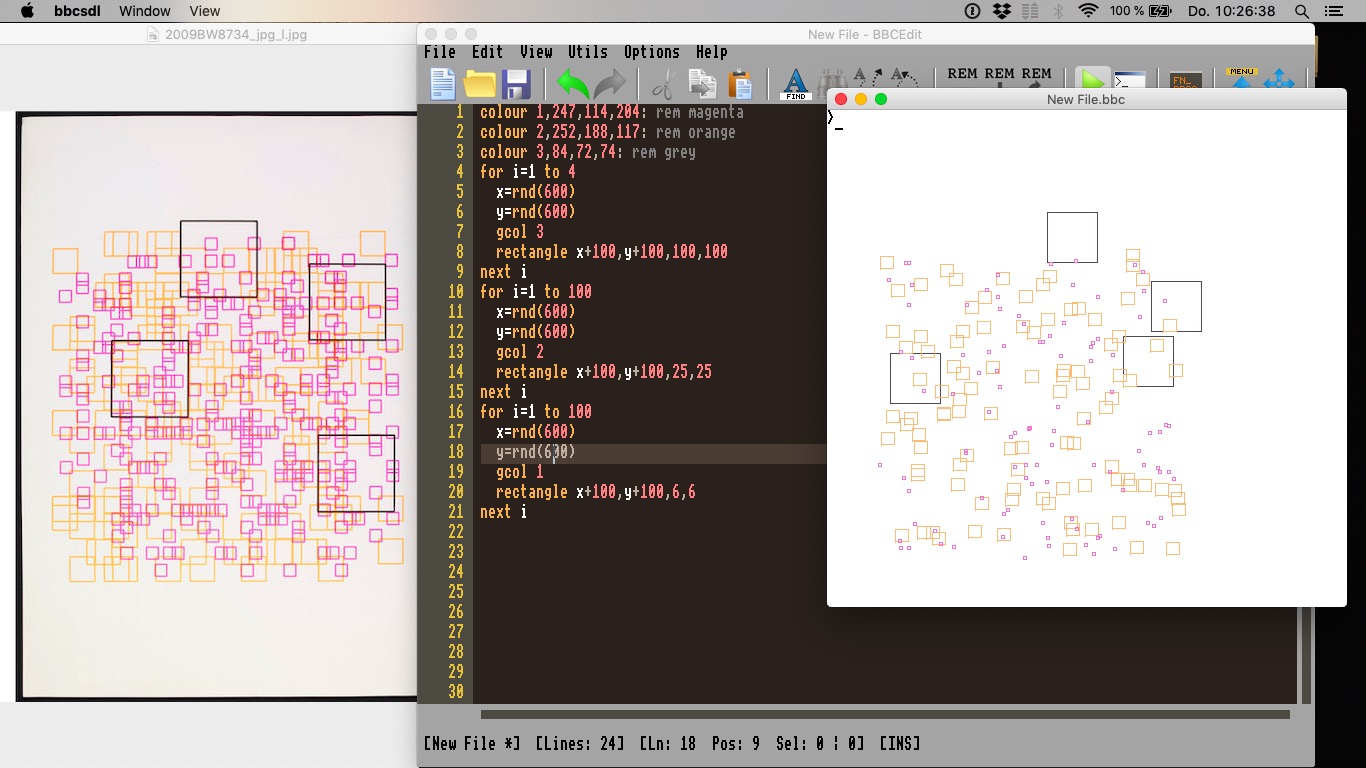
Abb. 6: Eine Ausgabe des Re-Enactments von “Quadrate”

Bei der Bearbeitung des Programms wurden die Farbdefinitionen zu Beginn vorgenommen, was ein Bereitlegen von Plotter-Farbstiften nachahmte. Zudem wurde, wie beim Noll-Re-Enactment, ein tastaturgesteuerter Neustart des Programms implementiert, um ohne großen Aufwand neue Varianten des Bildes generieren zu können.

clg
colour 1,247,114,204: rem magenta
colour 2,252,188,117: rem orange
colour 3,84,72,74: rem grey
for i=1 to 4
   gosub xy
   gcol 3
   rectangle x+100,y+100,100,100
next i
for i=1 to 100
   gosub xy
   gcol 2
   rectangle x+100,y+100,25,25
next i
for i=1 to 100
   gosub xy
   gcol 1
   rectangle x+100,y+100,6,6
next i
a$=get$
run
(xy)
   x=rnd(600)
   y=rnd(600)
return

4. Algorithmische Re-Enanctments

Eine Agenda der kybernetischen Kunst Ende der 1960er-Jahre war es, dem Computer zu einem positiveren Image zu verhelfen. War Rechnertechnik bis dahin vor allem aus dem Militär, der Wissenschaft und Wirtschaft bekannt und im öffentlichen Diskurs als ein Sinnbild kalter Rationalität vertreten, versuchten die Künstler der ersten Generation diese Nachteile in ihr Gegenteil umzudeuten: Die Präzision, Geschwindigkeit und Ausdauer, die Computer beim Abarbeiten von Algorithmen an den Tag legen, sollten als Werkzeuge für eine neue Kunstform nutzbar werden. Der rationalistischen Anspruch, der mit Computern verbunden war, floß in die Theorie zur Kunst ein: in die Informationsästhetik (siehe den ersten Teil dieses Beitrags).

Gerade der Begriff des Algorithmus fand zu dieser Zeit eine erste breite öffentliche Diskussion. Denn laut Jasia Reichardt (2008:72) und anderen sind nicht mehr die Bilder, sondern die hinter ihnen stehenden Algorithmen es, die die Kunstwerke darstellen. Dass in einem formalsprachlichen Ausdruck Kunstfertigkeit verborgen sein kann, war für eine technikskeptische Kunstwelt vielleicht der provoativste Gedanke, den die Informationsästhetik und die Kybernetik formulierten. (Nees berichtet von einem Disput, der sich 1965 an der TH Stuttgart zwischen ihm und dem Künstler Heinz Trökes zugetragen hat, bei dem Trökes monierte, dass der Computerkunst der “Duktus” fehle und Nees erwiderte, dass sich dieser programmieren ließe, sobald man wisse, was der Duktus sei. [Nees 2006:XIII].)

Der der kybernetischen Kunst innewohnende didaktische Impetus zeigt sich auch an der Präsentation der Werke durch ihre Autoren – insbesondere, wenn es um die Erklärung der Funktionen geht. Hier werden Algorithmen in vielfältigen Erscheinungsformen dazu genutzt, den Aufbau und die Entstehung einer Computergrafik zu erläutern. Zeitweise dienen sie sogar (wie bei Mohr [2014]) als regelrechte Bildunterschriften. Der zweite Re-Enactment-Teil des Kurses widmete sich solchen Beschreibungen, um daraus die Werke zu rekonstruieren. Dabei sollte en passant die Adäquanz der jeweiligen algorithmischen Beschreibung bewertet werden, was sich nicht zuletzt an der Ähnlichkeit zwischen Original-Grafik und Re-Enactment zeigen ließ.

4.1 “unambiguously in English”

Alan M. Turing konstatiert 1953, dass ein berechenbares Problem (also eines, für das ein Computer zur Lösung eingesetzt werden kann) keiner spezifischen Sprache zur Formulierung bedarf, um unzweideutig vermittelt werden zu können:

„If one can explain quite unambiguously in English, with the aid of mathematical symbols if required, how a calculation is to be done, then it is always possible to programme any digital computer to do that calculation, provided the storage capacity is adequate.“ […] „problem is reduced to explaining ‚unambiguously in English‘“ (Turing 1953:289)

Algorithmen lassen sich also auch in natürlichen Sprachen darlegen. Erst, wenn sie durch einen Computer abgearbeitet werden sollen, bedürfen sie einer techno-mathematischen Beschreibung in einer Programmiersprache. Diesen Gedanken schien auch Manfred Mohr verfolgt zu haben, der auf seiner Homepage und in Publikationen stichwortartige Beschreibungen seiner Bilder angibt, die den Entstehungs- und Entwicklungsprozess der dahinter stehenden Programme in deutscher Sprache angeben. Zu seinen 1969 entstandenen “Computer Generated Random Number Collages” heißt es:

“About the algorithm: Around a central line, random numbers determine the position, height, width, and existence of the rectangular white lines. This is a visual music collage, bringing to mind rhythm and frequencies.”

Dieser Text sollte dem ersten “Algorithmus-orientierten” Re-Enactment zugrunde liegen. Hierzu wurden die Kursteilnehmer zunächst gebeten, den Text in eine handgezeichnete Grafik zu überführen. Dabei entstanden Zeichnungen, die den Bildern (vgl. Abb. 7) ähnelten, aber in zentralen Details auch Unterschiede aufwiesen. Noch ohne den direkten Vergleich mit dem Original angestellt zu haben, wurden diese Zeichnungen als Grundlage für den Entwurf eines Computerprogramms verwendet. Dabei zeigte sich schnell, dass dem Text wichtige Informationen (etwa über die Menge, Positionierung und Farbe der “rectangles”) fehlen.

mode 1
origin 640,0
plot 0,0:draw 0,1024
for i=1 to 5
   y=rnd(1024)
   x=rnd(640)
   d=rnd(2)
   if d=1 then x=-x
   if d=2 then x=x: rem nicht notwendig
   h=rnd(205)
   w=rnd(640)-x
   rectangle fill x,y,w,h
next i

Abb. 7: Manfred Mohr: Computer Generated Random Number Collage Number 1 (1969)

Diese Angaben antizipierend entstanden Computergrafiken, die dem Original nur vage ähnelten (Abb. 8). Das Re-Enactment war damit zwar teilweise gescheitert, die Frage, ob Mohrs Beschreibungen tatsächlich alle Informationen für die Generierung der ihnen zugehörigen Bilder enthalten, negativ beantwortbar. Sie sind nur dem Namen nach “Algorithms”.

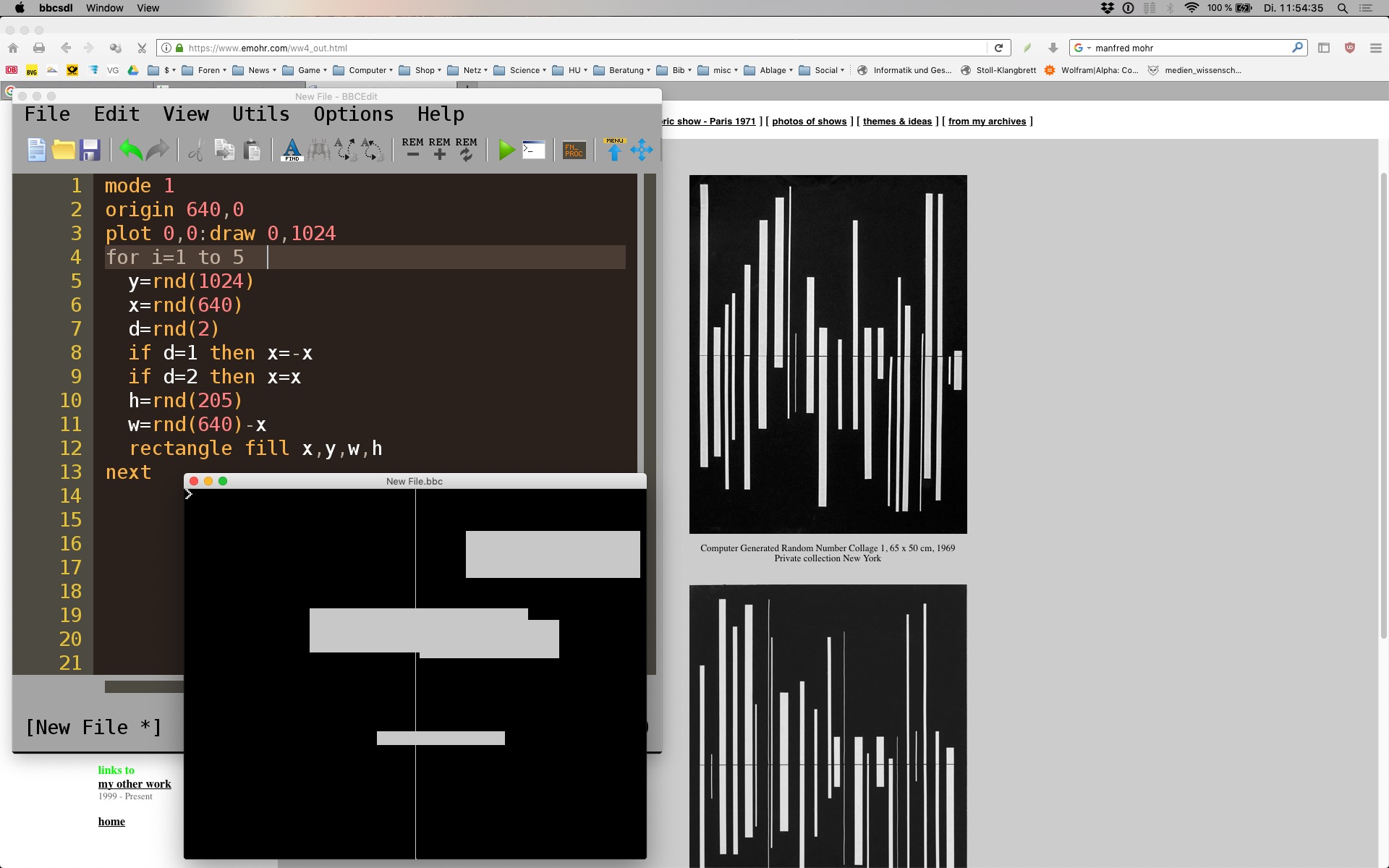
Abb. 8: Ausgabe eines Versuch des Re-Enactments

4.2 cybernetic/diagrammatic

Der “translation gap” zwischen natürlichsprachlicher Beschreibung, formalsprachlicher Kodierung und ikonischer Zeichnung eines Kunstwerks hatte vielleicht einen Anteil am Scheitern des ersten Versuchs. Vielleicht wäre ein Algorithmus, der dasselbe Zeichensystem (im Sinne Peirce) wie das Bild benutzt, daher adäquater? Dieser Versuch wurde mit der Übertragung eines Flussdiagramms von Frieder Nake in BBC BASIC vorgenommen. Dabei konnte zumindest ein Interpretationsprozess entfallen, denn im Wesen des Flussdiagramms liegt seine Unzweideutigkeit, die vor allem durch fest-definierte grafische Elemente erreicht wird.

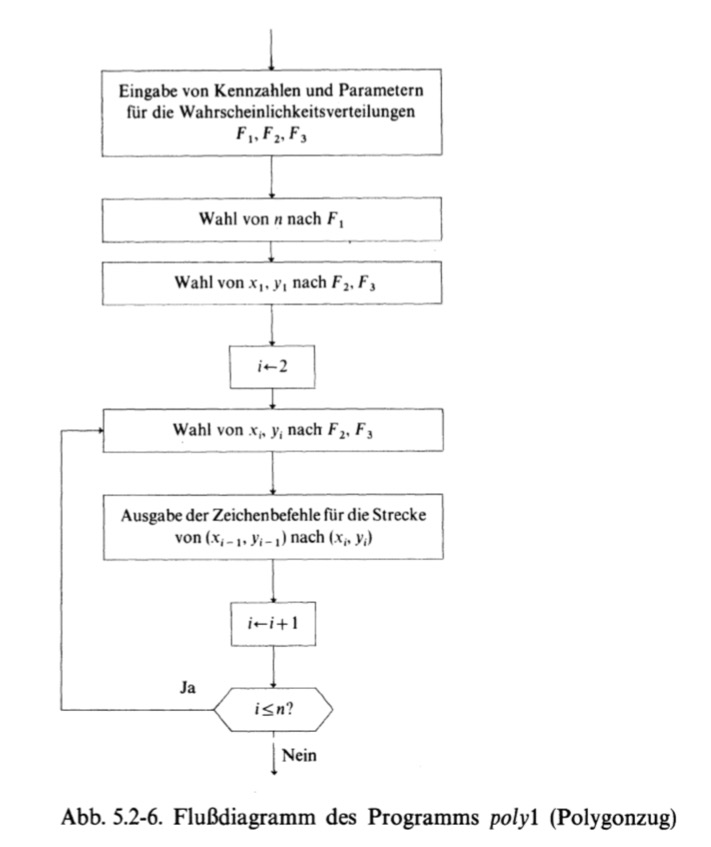
Abb. 9: Flussdiagramm des Programms poly1 (Polygonzug)

Das Beispiel entstammt Frieder Nakes Buch “Ästhetik als Informationsverarbeitung” [Nake 1974:198]. Nach einer kurzen Einführung in die Darstellungsweisen von Flussdiagrammen waren die Kursteilnehmer aufgefordert, das Diagramm mit BASIC-ähnlichem Pseudocode am Rand zu glossieren. Dies ermöglichte es die Zeitstruktur des Diagramms direkt in eine symbolische Struktur des Codes zu überführen. Hierbei zeigte sich, dass Missverständnisse oder gar fehlende Informationen nun keine Probleme mehr darstellten. Das BBC-BASIC-Programm zeichnete dann auch eine Grafik, die dem Beispielbild in Nakes Buch (1974:199) sehr ähnelte:

clg
dim x(100),y(100)
input f1
input f2
input f3
n=f1
x(1)=f2:y(1)=f3
i=2
(loop)
   x(i)=rnd(f2):y(i)=rnd(f3)
   move x(i-1),y(i-1):draw x(i),y(i)
   i=i+1
if i<n then goto loop
end

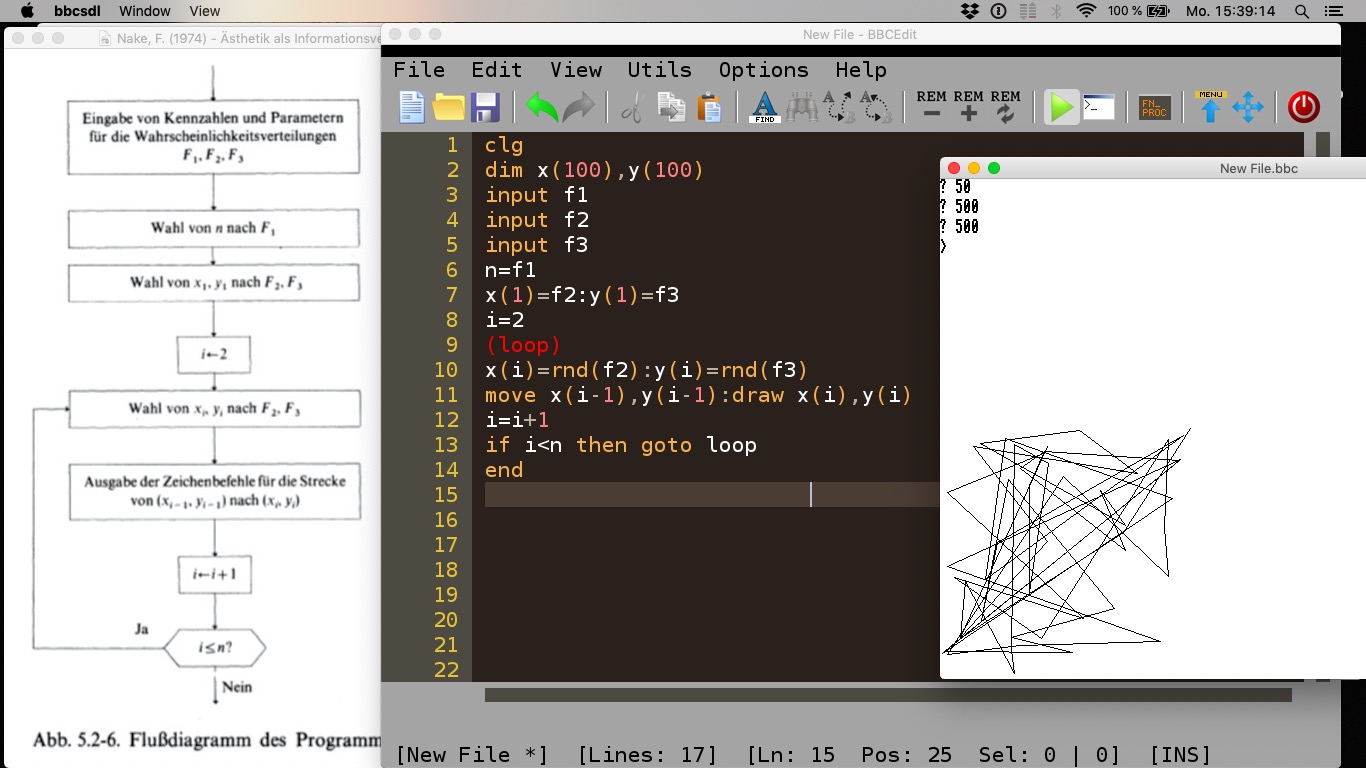
Abb. 10: “Zufälliger Polygonzug, 1963. 10 x 10 cm” (oben), Ausgabe des Re-Enactments (unten)

4.3 Code Translation

Das letzte Experiment konfrontierte die Kursteilnehmer mit einer in der Informatik schon seit längerem bekannten Problematik: Manche Computerprogramme müssen für aktuelle Systeme adaptiert werden, weil entweder die Originalhardware, auf der das Programm läuft/lief, nicht länger genutzt werden kann oder weil der Code aufgrund seines Alters (bzw. Des Alters der verwendeten Programmiersprache) nicht mehr sicher ist oder nicht mehr gewartet werden kann. Liegt der Sourcecode vor, kann eine Übersetzung in die Zielsprache von Hand durchgeführt werden, andernfalls muss der Objektcode rekompiliert (also durch den Computer übersetzt) werden.

Als Beispiel für diesen Prozess wurde ein Sourcecode aus Georg Nees Dissertation „Generative Computergrafik“ von 1969 ausgewählt. Die im Buch abgedruckten Programmcodes sind in einer Variante der Programmiersprache ALGOL verfasst. ALGOL war eines der Vorbilder bei der Entwicklung von BASIC, so dass die Programmstrukturen bereits sehr vertraut aussahen:

1 'BEGIN' 'COMMENT' SCHACHTELUNG., 2 'REAL' LI, RE, UN, OB, H.,
3 H.=.5., OPEN(0,0).,
4 LI.=-130.,RE.=130.,
5 UN.= -90., OB.=90.,
6 ANF..
7 LEER(0,OB)., LINE(LI,OB).,
8 LINE(LI,UN)., LINE(RE,UN).,
9 LINE(RE,OB)., LINE(0,OB).,
10 LINE(LI,0)., LINE(0,UN).,
11 LINE(RE,0)., LINE(0,OB).,
12 LI.=LI*H.,RE.=RE*H.,
13 UN.=UN*H.,OB.=OB*H.,
14 'IF' RE 'GREATER' 1.0 'THEN' 'GOTO' ANF., 15 CLOSE
16 'END' SCHACHTELUNG.,

Abermals wurde die Übersetzung in BBC BASIC als Glossierung des Originalcodes vorgenommen. Mit dem Hintergrundwissen der Verwandtschaft beider Programmiersprachen ließen sich hier einige der Überlegungen der BASIC-Entwickler direkt beim Umkodieren nachvollziehen – etwa, dass der Verzicht auf unterschiedliche Datentypen für Zahlen die Programmierung stark vereinfacht. Das resultierende BBC-BASIC-Programm stellte damit auch eine Form diachroner (Programmier)Sprachwissenschaft dar.

rem Schachtelung
origin 500,500
H=0.5:clg
LI=-130:RE=130
UN=-90:OB=90
(ANF)
   move 0,OB:draw LI,OB
   draw LI,UN:draw RE,UN
   draw RE,OB:draw 0,OB
   draw LI,0:draw 0,UN
   draw RE,0:draw 0,OB
   LI=LI*H:RE=RE*H
   UN=UN*H:OB=OB*H
if RE>1 then goto ANF
end

Die Richtigkeit der Translation ließ sich leicht anhand eines Vergleichs der Originalgrafik aus Nees‘ Buch und der Ausgabe des Re-Enactments belegen:

Abb. 11: G. Nees “Schachtelung (Bild 3)” (oben) + Re-Enactment (unten)

Damit war der praktische Teil des Kurses abgeschlossen. Weitere Re-Enactments ließen sicherlich neue und vertiefte Kenntnisse zur kybernetischen Kunst erwarten, erforderten aber auch erweiterte Kenntnisse der Programmierung in BBC-BASIC. So lassen die Arbeiten von Frieder Nake, Manfred Mohr oder Vera Molnar komplexe algorithmische Strukturen vermuten.

Ebenso erscheint es sinnvoll Werke der bildenden Kunst (etwa die Objekte Mohrs) im 3D-Druck-Verfahren oder Grafiken aus Analogcomputern (wie die frühen Werke Herbert W. Frankes) mit Hilfe solcher Systeme zu re-enacten. Dies würde jedoch bedeuten weitere techno-mathematische Kenntnisse vorbereiten zu müssen. Schließlich wäre es sicherlich sinnvoll den Fortgang der kybernetischen Kunst in Richtung Computergrafik und -animation weiterzuverfolgen. Dieser Punkt wurde im Kurs auf Basis von Referaten diskutiert.

5. Schluss: Vom kybernetischen zum künstlichen Künstler

Abb. 12: Bild aus der “Arnolfini”-Kollektion, gezeichnet von AARON (1983)

Der in einem Referat vorgestellte “Künstler” AARON bildete einen Kulminationspunkt für das Seminar. AARON ist eine künstliche Intelligenz, die, entwickelt von Harold Cohen, ab Anfang der 1980er-Jahre Computerkunst generierte. AARON eskaliert die Frage nach dem Algorithmus, weil sich aus dem Programmcode, der die Grundlage der KI ist, die von dieser entwickelten Kunstwerke nicht mehr “einfach” ablesen lassen. Sie bildet vielmehr die strukturelle Bedingung der Möglichkeit von datengetriebenen Grafiken. Damit suspendiert die Kybernetische Kunst zunächst auf der Produzentenseite das subjektive Moment (den menschlichen Künstler als Konstrukteur der Algorithmen). Von hier ab, so die Diskussion, führt eine direkte Linie einerseits zur Computer Generated Imagery (CGI), in der Computergrafik zur Gebrauchskunst wird; die andere Linie führt zu neueren Diskursen, wie den lernfähigen neuronalen Netzen, die in jüngerer Zeit auch damit befasst sind Kunst zu produzieren. (Vgl. Abb. 12)

Abb. 13: Portrait of Edmond Belamy, 2018, created by GAN (Generative Adversarial Network)

Wie das Bild zeigt, ist es nun nicht mehr die “Präzision” des Computer-Tools, die den Reiz des Werkes ausmacht, sondern genau ihr Gegenteil: eine Form von “künstlerischer Unpräzision”, die dem, was in der o.g. Nees-Debatte als “Duktus” bezeichnet wurde, schon recht nahe kommt. Dort hingegen, wo neuronale Netze nicht “Kunst” im Sinn haben, sondern fotorealistische Synthese, zeigen sich die (vielleicht letzten) Refugien der kybernetischen Kunst: Abb. 13 zeigt das künstliches Portrait einer Frau, die niemals existiert hat.

So verblüffend, wie diese Tatsache ist, verstört das Artefakt am rechten Bildrand. Der Algorithmus hat hier ein weiteres Gesicht zu generieren begonnen; die “Randbedingungen” des Formates haben jedoch dazu geführt, dass hier einiges “schief gelaufen” ist – ähnlich wie bei Nees Bild der “Locken”, die sich bei der Kollision mit dem materiellen Bildrand zu einem dunklen Rand verdichtet haben, ergeben hier die Daten des KI-Algorithmus dicht an den Rand gedrängt, die Kompressionsform eines Gesichts. Den Betrachter scheint es nicht zu stören, denn die Lernprozesse neuronaler Netze benötigen keine Subjekte zur Evaluation ihrer Outputs mehr. Menschliche Kritiker wären viel zu langsam, um den computerisierten Lernprozess zu regulieren. Es sind nun vielmehr zwei Computerprozesse, die hier gegeneinander antreten: Der eine als Künstler, der andere als sein Kritiker – in einem lediglich durch den Algorithmus gesteuerten Lern-Feedback-Prozess.

Abb. 14: “These Persons do not exist” (28.2.2019, 12:57 Uhr)

„Einen automatischen Künstler oder Kritiker zu konstruieren oder zu programmieren, steht zwar nicht an der Spitze der Liste von Aufgaben, wird aber früher oder später doch auch versucht werden.“ (Nake 1974:5)

(Englische Fassung)

Abbildungsverzeichnis:

• Abb. 1: “Vertical-Horizontal Number Three” (1965, A. Michael Noll), Quelle: http://collections.vam.ac.uk/item/O1193788/vertical-horizontal-number-three-photograph-noll-a-michael/ (16.03.2019)
• Abb. 2: Quelle: Stefan Höltgen
• Abb. 3: “Locken” (1971, Georg Nees), Quelle: http://dada.compart-bremen.de/item/artwork/994 (16.03.2019)
• Abb. 4: Quelle: Stefan Höltgen
• Abb. 5: “Quadrate” (1970, Herbert W. Franke), Quelle:  http://collections.vam.ac.uk/item/O192911/quadrate-squares-print-franke-herbert-w/ (16.03.2019)
• Abb. 6: Quelle: Stefan Höltgen
• Abb. 7: “Computer Generated Random Number Collage Number 1” (1969, Manfred Mohr), https://www.emohr.com/sc69-73/vfile_random69.html (15.03.2019)
• Abb. 8: Quelle: Stefan Höltgen
• Abb. 9: “Flussdiagramm des Programms poly1 (Polygonzug)” (Nake 1974:198)
• Abb. 10: Nake 1974:199
• Abb. 11: Nees 1969:99
• Abb. 12: Hardold Cohen/AARON “Arnolfini” (1983), https://dam-gallery.de/haroldcohen-preview/
• Abb. 13: Portrait of Edmond Belamy, 2018, created by GAN (Generative Adversarial Network), https://www.christies.com/features/A-collaboration-between-two-artists-one-human-one-a-machine-9332-1.aspx?sc_lang=en#FID-9332 (15.03.2019)
• Abb. 14: https://thispersondoesnotexist.com/ (28.02.2019)

Bibliografie:

• Collingwood, Robert G. (1947): “History as Re-Enactment”. In: Ders.: The Idea of History. Oxford University Press.
• Biancuzzi, F./Warden, S. (2009): Masterminds of Programming. Beijing u.a.: O’Reilly.
• Bogosts, Ian (2012): Alien Phenomenology. Or What it’s like to be a Thing. Minneapolis/London: Univ. of Minnesota Press.
• Fickers, Andreas (2015): “Hands-on! Plädoyer für eine experimentelle Medienarchäologie”, http://orbilu.uni.lu/handle/10993/21281
• Rheinberger, Hans-Jörg (2001): Experimentalsysteme und epistemische Dinge. Eine Geschichte der Proteinsynthese im Reagenzglas. Göttingen: Wallstein.
• Ernst, Wolfgang (2012): Chronopoetik. Zeitweisen und Zeitgaben technischer Medien. Berlin: Kadmos.
• Heidegger, Martin (1967): Sein und Zeit. Tübingen: Max Niemeyer Verlag.
• Nake, Frieder (1974): Ästhetik als Informationsverarbeitung. Grundlagen und Anwendungen der Informatik im Bereich ästhetischer Produktion und Kritik. Wien/New York: Springer.
• Nees, Georg (2006/1969): Visuelle Performanz. Einführung in den Neudruck des Buches Generative Computergraphik. In: Ders.: Generative Computergrafik. Herausgegeben von Hans-Christian von Herrmann und Christoph Hoffmann. Kaleidoskopien Band 6, S. IX-XXI.
• Mohr, Manfred (2014): Der Algorithmus des Manfred Mohr: Texte 1963-1979. Berlin: Spector.
• Turing, A. (1953): Digital Computers Applied to Games, http://eolo.cps.unizar.es/Docencia/doctorado/Articulos/ArticulosFamosos/1953%20Alan%20Turing-Digital%20Computers%20Applied%20to%20Games%20in%20book%20Bowden-FasterThanThought.pdf
• Reichardt, J. (2008): In the Beginning … In: Brown, P. (Ed): White Heat Cold Logic. British Computer Art 1960-1980. Cambridge/London: MIT Press, S. 71-82.