Feldgleichung

Der dritte Block unserer Rekonstruktion von „Tennis for Two“ ist heute zu Ende gegangen und hat leider fast nur aus „Debugging“ bestanden. Offenbar scheint etwas mit dem Analogcomputer nicht ganz in Ordnung zu sein. Wir haben dennoch ein paar Neuerungen getestet. Nach der Einbringung zweier externer Trimmpotenziometer und Trigger – passenderweise in Form der Atari CX-20-Paddles vorliegend – am gestrigen Tag, haben wir uns heute aufgeteilt. Ich war damit beschäftigt, die mathematische Funktion für das Tennisfeld als Schaltung auf einem anderen Analogrechner (einem Leyboldt-Haeraus-Lern-Analogcomputer) zu implementieren. Hier hat sich gezeigt, wie weit Theorie (Mathematik) und Praxis (Schaltung) auseinanderdriften können:

Während Higginbotham offenbar zwei getrennten Funktionen für den Boden des Spielfeldes und für das Netz implementiert hat, wollte ich die Sache „vereinfachen“. Dazu habe ich nach einer Gleichung gesucht, deren (später auf dem Oszilloskop dargestellter) Graph das Aussehen eines Tennisfeldes von der Seite hat – im Prinzip also dasselbe Erscheinungsbild wie Higginbothams Spielfeld. Gesucht war also eine Funktion, für die gilt:

-1<x<1 : y=0 \ x=0 : y=1

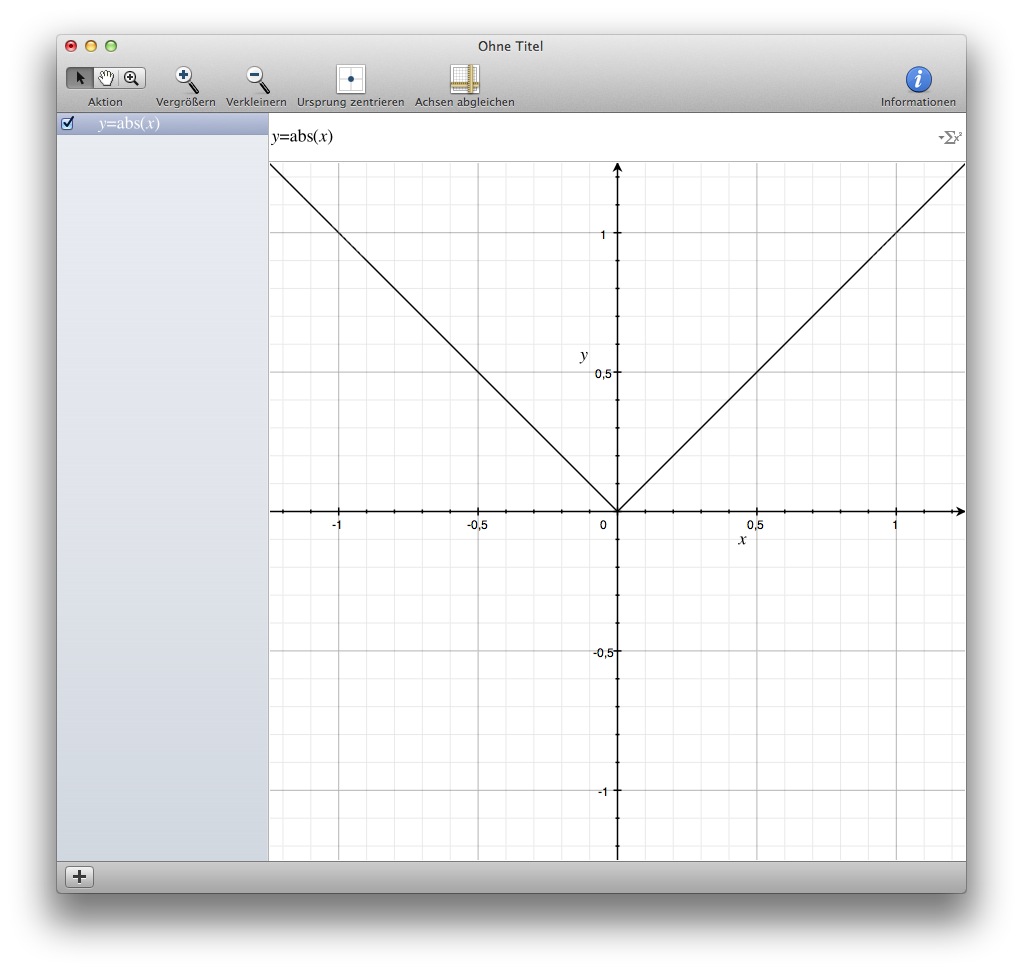
Also: An allen stellen eine Parallele zur X-Achse (die z.B. auch auf der X-Achse liegen kann); außer am Koordinatenursprung (y=0), wo sie auf den Wert x=1 springt. Für eine derartige, nicht stetige Funktion gibt es zwei Grundfunktionen: Die Betragsfunktion y=|x| (was auf manchen Computern als y=abs(x) darstellbar ist) sowie die Signum-Funktion y=sign(x). Erstere Funktion liefert grundsätzlich vorzeichenlose Werte für y, gleich welches Vorzeichen x hat:

Die Signumfunktion ist sozusagen die „umgekehrte“ Betragsfunktion. Sie ignoriert alle Werte von x und achtet stattdessen nur auf dessen Vorzeichen: Ist x negativ, dann ist y=-1, ist x positiv, dann ist y=1 und bei x=0 ist auch y=0. Der Graph dazu sieht folgendermaßen aus:

(Grau im Hintergrund wird noch y=|x| zum Vergleich angezeigt). Die Unstetigkeit dieser Funktion zeigt sich in x=0: Dort findet ein Sprung von y=-1 zu y=1 statt; der Graph liegt also genau auf der y-Achse des Koordinatensystems.

Nimmt man nun diese Signumfunktion und ermittelt ihren Betrag, stellt man also die Funktion y=abs(sign(x)) auf, dann erhält man einen Graphen, der parallel zur x-Achse bei y=1 verlauft und nur in x=0 zu y=0 springt:

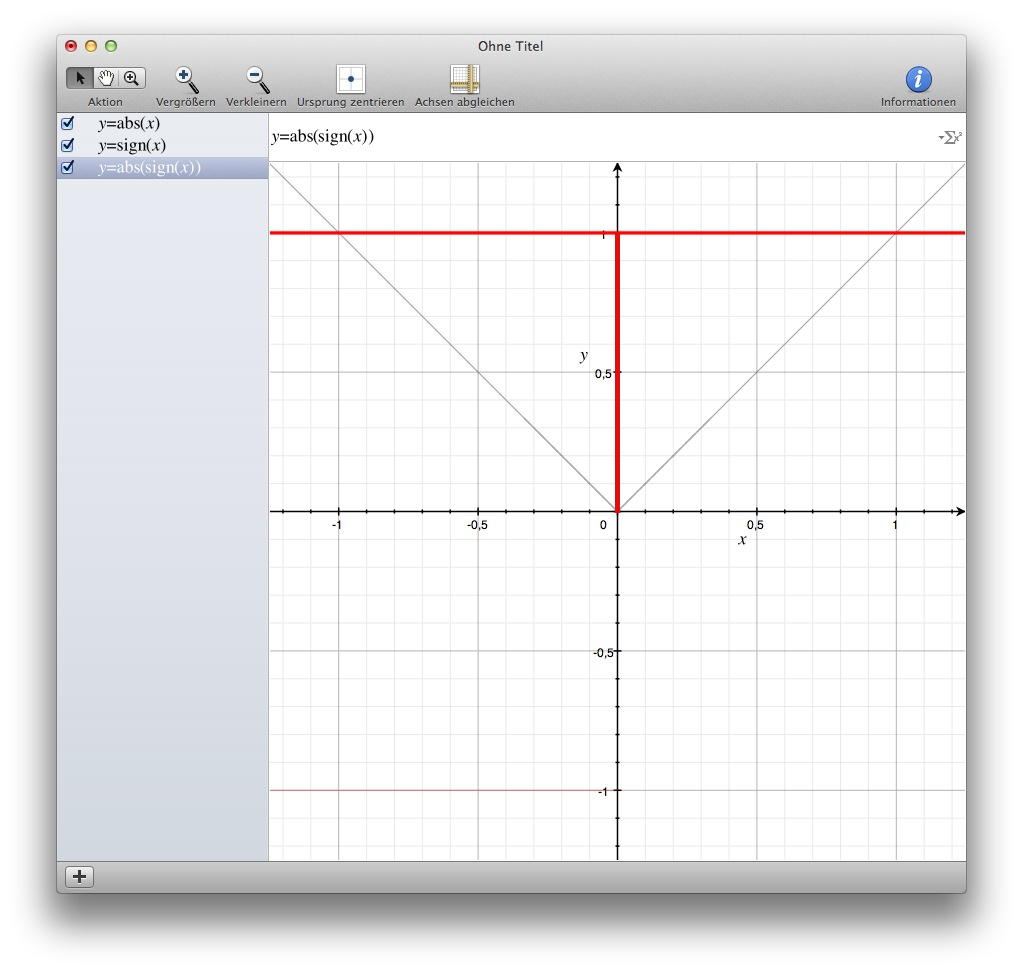Mit ein bisschen Fantasie betrachtet ist dieser (rot geplottete) Graph bereits ein auf dem Kopf stehendes, von der Seite gesehenes Tennisfeld. Das muss nun nur noch auf den Kopf gestellt werden, indem man es von 1 subtrahiert. Die Funktion heißt dann y=1-abs(sign(x)) und wird durch folgenden Graphen repräsentiert:

Dieser (grün geplottete) Graph wäre nun also elektronisch zu modellieren. Glücklicherweise gehören sowohl die Betrags- als auch die Signum-Funktion zu den häufig benötigten Schaltungen auf Analogcomputern, weswegen sie sich in dem meisten einführenden Werken und Handbüchern finden. So auch in dem des Leyboldt-Haeraus (S. 27-28). Wir mussten die Schaltungen nur noch aneinanderkoppeln, so dass die Ergebnisspannung der Signum-Funktion zur Eingangsspannung der Betragsfunktion wurde und deren Ergebnis (aufgrund der inversen Darstellung y=-sign(x), vgl. S. 28) noch einmal mit einer Schaltung mit -1 multipliziert wurde, damit wir auf den prinzipiellen Graphen kamen.

Prinzipiell, weil die Ergebnissumme noch von 1 subtrahiert werden muss (das wird noch implementiert) und weil wir natürlich noch einen „laufenden Wert“ für x benötigen, damit nicht nur ein Punkt, sondern der komplette Graph auf dem Oszilloskop erscheint. Den Hinweis für die Realisation dieser beiden Aspekte habe ich dankenswerter Weise von Bernd Ulmann bekommen (der uns sowieso wieder einmal sehr geholfen hat!) Zur Übergabe eines laufenden Wertes für x haben wir keine neue Sinus-Schaltung auf dem Analogcomputer gebaut (dazu fehlte uns eine Zenerdiode), sondern frecherweise einfach ein Sinus-Audiosignal von einem daneben stehenden eMac in die Schaltung eingegeben.

Wie sehr die praktischen Ergebnisse von den idealen mathematischen Vorlagen abweichen, ist erstaunlich:

Die Betragsfunktion

Sie Signum-Funktion

Die Verbindung der Schaltungen

Wie man leicht sieht, ist das kein Tennisfeld von der Seite. Der Graph ähnelt viel mehr einer gestreckten, inversen Signumfunktion. Wir haben bereits beim Test der einzelnen Funktionen festgestellt, dass diese in sehr unterschiedlichen Ergebnisbereichen liegen, das heißt, dass die Signumfunktion (oben rechts) viel größere y-Werte produziert als die Betragsfunktion (oben links). Das könnte ein Grund dafür sein, dass der Einfluss der Betragsfunktion auf das Ergebnis so „spärlich“ ist. (Unten links befindet sich eine angefangene Sinus-Funktion, die wir nicht genutzt haben).

In der kommenden Woche werde ich versuchen, dieses Problem zu beheben und dann natürlich hier davon berichten.